Question

The cylinder shown has a volume of 54π cm3. In a similar cylinder, the dimensions have been doubled. What is the ratio of the volumes (small to large)?

Answer 1

The answer to the problem is 1:8

Answer 2

1: 8

Explanation:

Volume of a cylinder(V) is given by:

`V = \pi r^2h`

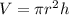
where,

r is the radius and h is the height of the cylinder.

As per the statement:

Let V and V' be the volume of small cylinder and large cylinder.

The small cylinder has a volume of 54π cm^3.

⇒
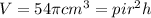`V =54 \pi cm^3= pi r^2h` ....[1]

It is also given:

In a similar cylinder, the dimensions have been doubled

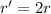`r' = 2r` and
`h' = 2h`

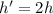
then, volume for large cylinder we get;

`V' = \pi (2r)^2(2h) = 8 \pi r^2h`

⇒
`V' = 8V`

⇒
`(V)/(V') = (1)/(8)`

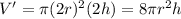
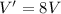
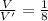
⇒V : V' = 1 : 8

Therefore, the ratio of the volumes (small to large) is, 1: 8