Question

The amount of time it takes to see a doctor a CPT-Memorial is normally distributed with a mean of 33 minutes and a standard deviation of 12 minutes. What is the Z-score for a 42 minute wait?

Use the following information to find the Z- score.



⎯⎯⎯⎯⎯
X
¯
⎯⎯⎯⎯⎯
X
¯
= 82


μ

μ
= 89


σ

σ
= 1

n = 22





Round your answer to two decimal places.





Round your answer to two decimal places.

Answer 1

a) Z-score = 0.75

b) Z-score = -32.833

Explanation:

Step(i):-

Given that mean of the Population = 33

Given a standard deviation of the Population = 12

Let 'X' be a random variable in a normal distribution

Let 'X' = 42

Step(ii):-

`Z = (x-mean)/(S.D)`

`Z = (42-33)/(12) = 0.75`

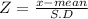
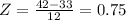
Step(iii):-

Given that mean of the Population = 89

Given a standard deviation of the Population = 1

Let 'X' be a random variable in a normal distribution

Let 'X⁻ = 82

`Z = (x^(-) -mean)/((S.D)/(√(n) ) )`

`Z = (82-89)/((1)/(√(22) ) ) = -32.833`

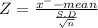
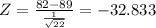
Z-score = -32.833