What are the angle measures of the triangle 6 12 6sqrt3?

Question

asked Apr 12, 2019 207k views

1 Answer

Luukes · Answer 1 · 2019-04-16T11:45:12+0000

Answer:

The measure of angle A is 30 degree, measure of angle B is 90 degree and measure of angle C is 60 degree.

Explanation:

The measures of given sides are 6, 12,
6√(3) .

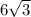According to the Law of Cosine:

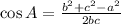
$\cos A=(b^2+c^2-a^2)/(2bc)$

Using Law of Cosine, we get

$\cos A=((12)^2+(6√(3))^2-(6)^2)/(2(12)(6√(3)))$

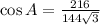
$\cos A=(216)/(144√(3))$

$\cos A=(3)/(2√(3))$

$\cos A=\frac{√(3){2}$

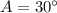
$A=30^(\circ)$

Similarly,

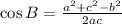
$\cos B=(a^2+c^2-b^2)/(2ac)$

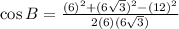
$\cos B=((6)^2+(6√(3))^2-(12)^2)/(2(6)(6√(3)))$

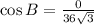
$\cos B=(0)/(36√(3))$

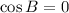
$\cos B=0$

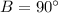
$B=90^(\circ)$

Therefore, measure of angle A is 30 degree and measure of angle B is 90 degree.

According to angle sum property, the sum of interior angles of a triangle is 180 degree.

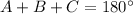
$A+B+C=180^(\circ)$

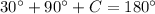
$30^(\circ)+90^(\circ)+C=180^(\circ)$

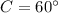
$C=60^(\circ)$

Therefore the measure of angle C is 60 degree.