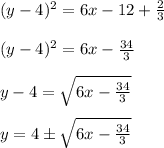Question

Helpppppppppppppppppp

Answer 1

The inverse of a function is what reverses it. That is, if a function outputs y for an input x, then its inverse will output x for an input y.

To find the inverse of a function, we interchange x and y in the equation.

Here, we have
`(x-4)^2- (2)/(3) = 6y-12`.

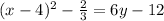
We first interchange x and y.


`(y-4)^2- (2)/(3) = 6x-12`

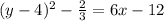
This form is technically an inverse already, but by convention and for the answer choices, we will now solve for y.


`(y-4)^2= 6x-12+(2)/(3) \\ \\ (y-4)^2 = 6x- (34)/(3) \\ \\ y-4= \sqrt{6x-(34)/(3)} \\ \\ y = 4\pm\sqrt{6x-(34)/(3)}`