Question

Helpppppppppppppppppppppppppppppppppppp

Answer 1

It might be tempting at first to set each factor equal to nine and solve for x, but we can't do that because the zero product property only works for factors equal to zero. So, we must expand the two binomials, and then complete the square as asked.


`(x-12)(x+4)=9 \\ \\ x^2-8x-48=9 \\ \\ x^2-8x=57`

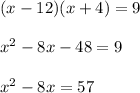
Completing the square is like forcing a quadratic to be factored as a perfect square trinomial. To do that, we add
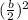
`( (b)/(2))^2` to both sides of the equation.
`( (b)/(2))^2 = (-4)^2=16`

`x^2-8x+16=57+16`

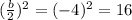
Next, we factor as a perfect square trinomial and simplify the righthand side.


`(x-4)^2=73`


`x-4=\pm√(73)\\\\x=4\pm√(73)`

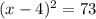
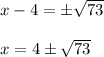The answer is C.