The gravitational acceleration on the surface of planet A is:
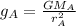
where G is the gravitational constant,
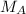
is the mass of planet A and

its radius.
Similarly, the gravitational acceleration on the surface of planet B is:
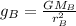
The ratio between the gravitational acceleration on planet A and B becomes:
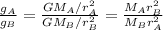
The problem says that the two masses are equal:
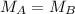
while planet A has 3 times the radius of planet B:
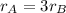
. Substituting into the ratio, we get:
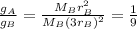
so, gravity on planet B is 9 times stronger than planet A.