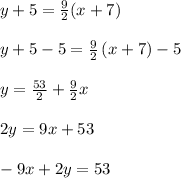Question

1. A line passes through (-7 -5) and (-5 4).

A. Write an equation for the line in point-slope form
B. Rewrite the equation in standard form using integers

Answer 1

`y=(9)/(2)x+[tex](53)/(2)`

`9x-2y=-53`

Explanation:

The line is passing through
`(-7,-5)` and
`(-5,4)`.

The equation of line in point-slope form can be obtained by using the following rule that says:

`(y-y_1)=m(x-x_1)`

Lets say:
`(x_1,y_1),(x_2,y_2)` are
`(-7,-5)` and
`(-5,4)` respectively.

Lets find the slope of the line:

`m=(y_2-y_1)/(x_2-x_1) =(4-(-5))/(-5-(-7)) =(4+5)/(-5+7)=(9)/(2)`

So the slope of the line is
`(9)/(2)`.

`(y-(-5))=(9)/(2)(x-(-7))`

`y+5=(9)/(2)(x+7)`

`y=(9)/(2)x+[tex](9)/(2)* 7`-5=\frac{9}{2}x+
`(53)/(2)`

`y=(9)/(2)x+[tex](53)/(2)`

So the required equation is
`y=(9)/(2)x+[tex](53)/(2)`.

And the equation of line in standard form can be written as:

`(-9)/(2)x+y=[tex](53)/(2)`

Multiplying the equation by 2 we get:

`-9x+2y=53`

`9x-2y=-53`

Answer 2

The point-slope form is
`y+5=(9)/(2) (x+7)`.

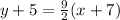The standard form of a line is
`-9x + 2y = 53`.

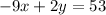Explanation:

Point-slope is a specific form of linear equations in two variables:

`y-b=m(x-a)`

When an equation is written in this form,
`m` gives the slope of the line and
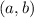`(a,b)` is a point the line passes through.

To find the line that passes through the points
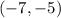`(-7, -5)` and
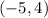`(-5, 4)`. First, we use the two points to find the slope:

`m=(4-(-5))/(-5-(-7)) =(9)/(2)`

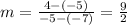
Now we use one of the points, let's take
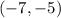`(-7, -5)`, and write the equation in point-slope:

`y+5=(9)/(2) (x+7)`

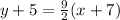
The standard form of a line is in the form
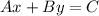`Ax + By = C` where A is a positive integer, and B, and C are integers.

To find this form you must

`y+5=(9)/(2) (x+7)\\\\y+5-5=(9)/(2)\left(x+7\right)-5\\\\y=(53)/(2)+(9)/(2)x\\\\2y=9x+53\\\\-9x+2y=53`