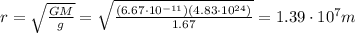Question

On the surface of planet y, which has a mass of 4.83x1024 kg, a 30.0 kg object weighs 50.0 n. what is the radius of the planet?

Answer 1

We can solve the problem in two steps:

1) From the weight W=50.0 N of the object, we can find the value of the gravitational acceleration g of the planet. In fact, the weight is equal to

`W=mg`
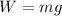
where m=30 kg is the mass of the object. From this, we find g:

`g= (W)/(m)= (50.0 N)/(30 kg)=1.67 m/s^2`

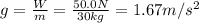
2) The gravitational acceleration of a planet with mass M and radius r is given by

`g= (GM)/(r^2)`
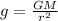
where
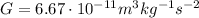
`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constant. In our problem, the mass of the planet is

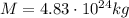
`M=4.83 \cdot 10^(24) kg`, and we found g in step 1),
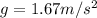
`g=1.67 m/s^2`, so we have everything to solve and find the value of the radius r:

`r= \sqrt{ (GM)/(g) }= \sqrt{ ((6.67\cdot 10^(-11))(4.83 \cdot 10^(24)))/(1.67) }=1.39\cdot 10^7 m`