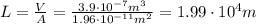Question

Gold, which has a density of 19.32 g/cm3, is the most ductile metal and can be pressed into a thin leaf or drawn out into a long fiber. (a)if a sample of gold with a mass of 7.583 g, is pressed into a leaf of 3.061 μm thickness, what is the area (in m2) of the leaf? (b)if, instead, the gold is drawn out into a cylindrical fiber of radius 2.500 μm, what is the length (in m) of the fiber?

Answer 1

(a) First of all, let's convert the gold's density into appropriate units:

`d=19.32 g/cm^3 = 19320 kg/m^3`
and the mass as well:

`m=7.583 g=7.583 \cdot 10^(-3) kg`
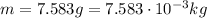
From density and mass, we can find the volume of the leaf, V:

`V= (m)/(d)= (7.583 \cdot 10^(-3) kg)/(19320 kg/m^3) =3.9\cdot 10^(-7)m^3`
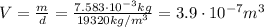
We know that the thickness is
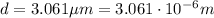
`d=3.061 \mu m=3.061 \cdot 10^(-6) m`, and the volume is the product between the thickness and the area:
`V=A d`, so we can find the area:

`A= (V)/(d)= (3.9\cdot 10^(-7)m^3)/(3.061 \cdot 10^(-6) m) =0.127 m^2`

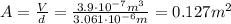
(b) The radius of the cylinder is
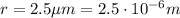
`r=2.5 \mu m=2.5 \cdot 10^(-6) m`, therefore its area is

`A=\pi r^2 = 1.96\cdot 10^(-11) m^2`
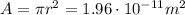
For a cylinder, the volume is the product between the length L and the area A: V=AL, therefore we can find the length L (the volume is the one calculated at the previous step):

`L= (V)/(A) = (3.9\cdot 10^(-7)m^3)/(1.96\cdot 10^(-11) m^2) =1.99\cdot 10^4 m`