The impulse of a force is defined as
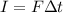
where F is the intensity of the force and
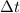
the time of application of this force.
We can rewrite the previous relationship by using Newton's second law:
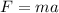
substituting, the equation for the impulse becomes
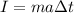
But the acceleration is the variation of the velocity in the time interval:
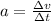
so we can rewrite I as
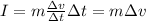
the combined mass of sled and rider is m=74 kg, while the variation of velocity is
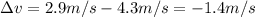
and so we can calculate the impulse of the friction force:
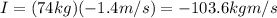
where the negative sign means the friction force acts against the motion, to decelerate the system.