Question

Use algebra tiles to model and solve x+5=3x-1

Answer 1

The question asks that you use algebra tiles to model and solve the equation
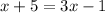
`x+5=3x-1`. I set up the scenario digitally (see attached image).

Whatever blocks you have on both sides you can cancel. So we cancel one
`x`-block, and to take away the
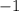
`-1`-block, we balance the equation by putting a
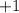
`+1`-block on the other side. We are left with 2
`x`-blocks equal to 6
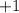
`+1`-blocks. This is equivalent to 1
`x`-bock equal to 3
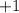
`+1` blocks, so
`x=3`.

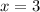
Algebraically, you can write

`x+5=3x-1 \\ 5=2x-1 \\ 6=2x \\ x=3`.
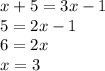
I personally find the latter approach much easier, but I think the tiles are a nice way to conceptualize what you're doing.

Answer 2

x + 5 = 3x - 1
x - 3x = -1 -5
-2x = -6
2x = 6
x= 6÷ 2
x = 3