Question

The 2779-m Brooklyn-Battery Tunnel, connecting Brooklyn and Manhattan, is one of the world's longest underwater vehicular tunnels. (a) Determine its fundamental frequency of vibration. (b) What harmonic must be excited so that it resonates in the audio region at 20 Hz or greater?

Answer 1

For a cylinder that has both ends open resonant frequency is given by the following formula:

`f= (nv)/(2L)`
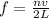
Where n is the resonance node, v is the speed of sound in air and L is the length of a cylinder.
The fundamental frequency is simply the lowest resonant frequency.
We find it by plugging in n=1:

`f_0= (v)/(2L)=(343)/(2\cdot 2779)=0.062 Hz`
To find what harmonic has to be excited so that it resonates at f>20Hz we simply plug in f=20 Hz and find our n:

`20= (n343)/(2\cdot 2779) =n\cdot f_0`
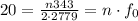
We can see that any resonant frequency is simply a multiple of a base frequency.
Let us find which harmonic resonates with the frequency 20 Hz:

`20=n\cdot f_0\\ n=(20)/(0.062)=322.58`
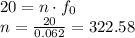
Since n has to be an integer, final answer would be 323.