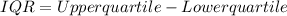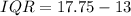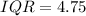Question

These data show the age in years of 9 members of the youth orchestra.

12 14 16 17.5 10 18 15 15.5 19

What is the IQR (interquartile range) for these data?


4.75

9.00

15.50

17.75

Answer 1

Hey there!

the answer is 4.75.

4.75 is the IQR for the data

Hopes this helps u :)

Answer 2

`IQR=4.75`

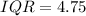
Explanation:

The given data is:

12,14,16,17.5,10,18,15,15.5,19

In order to find the interquartile range, we have to arrange the given data set in ascending order, thus

10, 12, 14, 15, 15.5, 16, 17.5, 18, 19

Now, the lower quartile is: 10, 12, 14, 15

Median is given as:

`M=(14+16)/(2)=(26)/(2)=13`

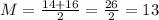
And the upper quartile is given as:

16, 17.5, 18, 19

Median is given as:

`M=(17.5+18)/(2)=17.75`

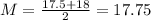
thus, the Interquartile range is given as:

`IQR=Upper quartile-Lower quartile`

`IQR=17.75-13`

`IQR=4.75`