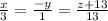The intersection line of two planes is the cross product of the normal vectors of the two planes.
p1: z=4x-y-13 => 4x-y-z=13
p2: z=6x+5y-13 => 6x+5y-z=13
The corresponding normal vectors are:
n1=<4,-1,-1>
n2=<6,5,-1>
The direction vector of the intersection line is the cross product of the two normals,
vl=
i j k
4 -1 -1
6 5 -1
=<1+5, -6+4, 20+6>
=<6,-2,26>
We simplify the vector by reducing its length by half, i.e.
vl=<3,-1,13>
To find the equation of the line, we need to find a point on the intersection line.
Equate z: 4x-y-13=6x+5y-13 => 2x+6y=0 => x+3y=0.
If x=0, then y=0, z=-13 => line passes through (0,0,-13)
Proceed to find the equation of the line:
L: (0,0,-13)+t(3,-1,13)
Convert to symmetric form:
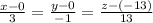
=>