Question

Find the orbital period (in years) of an asteroid whose average distance from the sun is 5 au.

Answer 1

By equating the centripetal force and the gravitational pull, we have the equation


`(mv^2)/(r)=(GMm)/(r^2)`
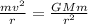
where
G=gravitational constant=6.67408*10^(-11) (m^3 kg^-1 s^-2)
m=mass of object
M=mass of sun=1.9885*10^(30) (kg)
v=tangential velocity of object
r=distance from the sun (m)

On simplification, we get the relation

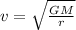
`v=\sqrt{(GM)/(r)}` (m/s)
Subtituting constants,including
1 au = 1.49597870700*10^(11) m
and given
r=5 au = 7.47989*10^11 m

`v=\sqrt{(GM)/(r)}`

`=\sqrt{(1.32712*10^(20))/(7.47989*10^(11))}`

`=√(1.774250*10^8)`

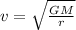
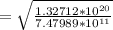
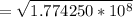
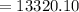
`=13320.10` m/s

Therefore the orbital period is

`T=(2\pi(5*au))/(13320.10)` s

`=(2\pi(5*au))/(13320.10*365.25*86400)` years

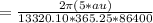
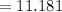
`=11.181` years