Question

Help! How do you graph transformations of the square-root graph?

Answer 1

The parent function
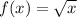
`f(x)= √(x)` is simplest. It looks like half a parabola turned by 90°. It starts at the origin, and when you're graphing, it's best to look for values x that are perfect squares, e.g., plot (4,2) and (9,3). Draw a smooth curve to connect the points you've drawn. Note that it's range is [0, ∞).

For transformations, there are some general rules that apply to many other functions.

Let's look at shifts involving a constant number 5.

If you write
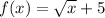`f(x)= √(x) +5`, this moves the whole graph up 5 units. Think about it... For each value f(x) you have from the parent function, just add 5.

If you write
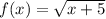`f(x)= √(x+5)`, this corresponds to a shift 5 units to the left, or in the negative direction, so that your graph now starts at (-5,0), and otherwise does all the same things. Likewise,
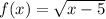`f(x)= √(x-5)` corresponds to a shift 5 units to the right.

If you write
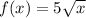`f(x)=5 √(x)`, this multiplies every value f(x) times 5. So, as you can imagine, everything is stretched vertically by a factor of 5 (imagine it gets taller). When you're graphing, you need to carefully scale your axes and graph and label the parent function for comparison. *Note that I chose 5 as our constant number c. If we choose any number greater than 1, it's a stretch, and if we choose any number less than 1, it's a compression.

If you write
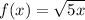`f(x)= √(5x)`, everything gets stretched horhzatonally (it gets wider). For c greater than 1, it's a stretch. For c less than 1, it's a compression.

See the attached graphs for an illustration.