The domain of a(x) is all of R. The domain of b is the range where
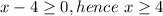
. We can calculate the composition boa by changing in the expression for b, every x with a(x). Hence, boa(x)=
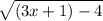
=
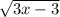
. Again for a function with a root to be defined, we need that the expression under the square root has to be positive. Hence, 3x-3
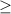
0.Thus, the set where this holds is
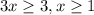
. This is also the domain of the function boa(x).