Question

A plane takes off in san francisco at noon and flies toward the southeast. an hour later, it is 400 kilometers east and 300 kilometers south of its starting location. assuming the plane flew in a straight line, how far did it travel? how many degrees south of east did the plane fly?

Answer 1

This first step involves a right triangle. If the plane is 400 km east and 300 km south of the origin, and it flew in a straight line, then you can construct a right triangle with side lengths 300, 400, and c. You may recognize that these are multiples of the Pythagorean triple 3, 4, 5, so the side length c is 500 km. Otherwise, you would write

`c^2 = 300^2+400^2 \\ c = 500`.

This second step is, if I am correctly interpreting "degrees south of east," to find the angle formed by the horizontal line representing the east and the path of the plane. I made a diagram that does just that (see attached). You can use a trig function of one of the angles to solve. I chose

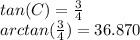
`tan(C)= (3)/(4) \\ arctan( (3)/(4))=36.870`. Thus, I believe it is 37° south of east.