Question

The length of time that an auditor spends reviewing an invoice is approximately normally distributed with a mean of 600 seconds and a standard deviation of 100 seconds. what is the probability that an auditor will spend more than 12 minutes on an invoice?

Answer 1

Answer: 11.5%

Step-by-step explanation:

Since 1 minute = 60 seconds, we multiply 12 minutes by 60 so that 12 minutes = 720 seconds. Thus, we're looking for a probability that the auditor will spend more than 720 seconds.

Now, we get the z-score for 720 seconds by the following formula:


`\text{z-score} = (x - \mu)/(\sigma)`

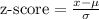
where


`t = \text{time for the auditor to finish his work } = 720 \text{ seconds} \\ \mu = \text{average time for the auditor to finish his work } = 600 \text{ seconds} \\ \sigma = \text{standard deviation } = 100 \text{ seconds}`

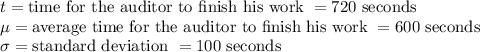
So, the z-score of 720 seconds is given by:


`\text{z-score} = (x - \mu)/(\sigma) \\ \\ \text{z-score} = (720 - 600)/(100) \\ \\ \boxed{\text{z-score} = 1.2}`

Let

t = time for the auditor to finish his work
z = z-score of time t

Since the time is normally distributed, the probability for t > 720 is the same as the probability for z > 1.2. In terms of equation:


`P(t \ \textgreater \ 720) \\ = P(z \ \textgreater \ 1.2) \\ = 1 - P(z \leq 1.2) \\ = 1 - 0.885 \\ \boxed{P(t \ \textgreater \ 720) = 0.115}`

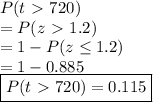
Hence, there is 11.5% chance that the auditor will spend more than 12 minutes in an invoice.