Question

A ball is tossed from an upper-story window of a building. the ball is given an initial velocity of 7.90 m/s at an angle of 18.0° below the horizontal. it strikes the ground 4.00 s later. (a) how far horizontally from the base of the building does the ball strike the ground? 30.04 correct: your answer is correct. m (b) find the height from which the ball was thrown. incorrect: your answer is incorrect. work only with the vertical components of these quantities. this part of the problem is then a 1-dimensional free-fall example. m (c) how long does it take the ball to reach a point 10.0 m below the level of launching? s

Answer 1

In order to solve the problem, let's write the equations of motion first. Let's take the x-axis as the horizontal direction, and the y-axis on the vertical direction (pointing downward). Calling
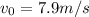
`v_0=7.9 m/s` the initial velocity, and
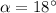
`\alpha=18^(\circ)` the angle below the horizontal, the equations of motion are

`S_x(t)=v_0 cos (\alpha )t`

`S_y(t)=v_0 sin (\alpha ) t+ (1)/(2)gt^2`
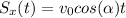
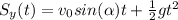
where
`g=9.81 m/s^2` is the gravitational acceleration.

(a) To find the distance covered by the ball horizontally, we must simply calculate Sx at the time the ball hits the ground (t=4.0 s):

`S_x(4.0s)= 7.9 m/s \cdot cos (18^(\circ)) \cdot 4.0s=30.05 m`

(b) The height from which the ball was thrown is the value of Sy at 4.0s, which is the distance covered by the ball before hitting the ground:

`S_y(4.0 s)=7.9 m/s \cdot sin(18^(\circ)) \cdot 4.0s + (1)/(2)(9.81 m/s^2)(4.0s)^2=88.24 m`

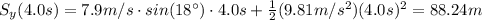
(c) To calculate how long does it take to the ball to reach 10.0 m below the initial point, we have to find the time at which Sy(t)=10.0 m. This means we must solve the following equation:

`10.0m = v_0 sin (\alpha ) t + (1)/(2) gt^2`
Using the data of the problem, we can solve this equation. We find two solutions for t: one is negative, so we can neglect it. The second one, which is the solution of the problem, is t=1.19 s.