Question

A machinist creates a washer by drilling a hole through the center of a circular piece of metal. If the piece of metal has a radius of x + 7 and the hole has a radius of x + 6, what is the area of the washer?

Answer 1

The area of the washer (which is a circle, but the inner part cut out) is given by:

`A_c = \pi r^2`

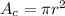
Now, we need to find the radius of the entire metal circle which the hole was drilled on:

`R_w = (x+7) - (x+6) = 1`

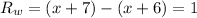
Plug it in to find the area of the metal plate:

`A_p = \pi (1)^2 = \pi`

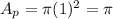
Now, you subtract the area of the hole from the area of the plate. The area of the hole will be:

`A_h = \pi (x+6)^2`

`A_h = \pi (x^2+12x+36) =`

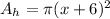
Subtract the area of the hole from the metal plate to get:

`A_w = \pi - (\pi x^2+12 \pi x+36 \pi) = \pi x^2+12 \pi x -35 \pi`

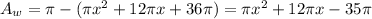
That's your answer, although it looks wrong because not much information was provided.