Question

A city council consists of six democrats and five republicans. If a committee of seven people is selected, find the probability of selecting four Democrats and three republicans.

Answer 1

Use hypergeometric distribution where there are two categories of identical objects/persons, each with a know size.
d=number of Democrats selected
D=total number of Democrats = 6
r=number of Republicans
R=total number of Republicans =5
Then

`P(d,r)=(C(D,d)C(R,r))/(C(D+R,d+r))`
where

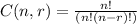
`C(n,r)=(n!)/((n!(n-r)!))` = combination of r items selected from n,
D+R=total number of members = 6+5 =11
d+r=number of members selected = 7


`P(d,r)=(C(D,d)C(R,r))/(C(D+R,d+r))`

`P(4,3)=(C(6,4)C(5,3))/(C(6+5,4+3))`

`=(C(6,4)C(5,3))/(C(11,7))`

`=(15*10)/(330)`

`=(5)/(11)`

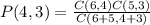
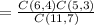
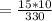
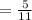
Answer: the probability of selecting 4 Democrats and 3 Republicans is 5/11