Question

A pharmacist has an 18% alcohol solution and a 40% alcohol solution. How much of each should he mix together to make 10 liters of a 20% alcohol solution?

Answer 1

x = amount of the 18% solution

y = amount of the 40% solution

we know the 18% solution has only 18% of alcohol, the rest is maybe water or something, now, how many liters is 18%? well, 18% of anything is just (18/100) * anything, so, 18% of x is just (18/100) *x or 0.18x, and that's how many liters are there.

likewise, how many liters are there in the 40% solution? well, (40/100) * y, or 0.4y, that many.

we know the mixture has to yield 10 liters at 20% alcohol, how many liters of only alcohol is that? well, (20/100) * 10, or 2 liters.


`\bf \begin{array}{lccclll} &\stackrel{liters}{amount}&\stackrel{alcohol~\%}{quantity}&\stackrel{liters}{alcohol}\\ &------&------&------\\ \textit{18\% solution}&x&0.18&0.18x\\ \textit{40\% solution}&y&0.40&0.4y\\ ------&------&------&------\\ mixture&10&0.20&2 \end{array}`


`\bf \begin{cases} x+y=10\implies \boxed{y}=10-x\\ 0.18x+0.4y=2\\ ----------\\ 0.18x+0.4\left( \boxed{10-x} \right)=2 \end{cases} \\\\\\ 0.18x-0.4x+4=2\implies -0.22x=-2 \\\\\\ x=\cfrac{-2}{-0.22}\implies x=\cfrac{100}{11}\implies x=9(1)/(11)`

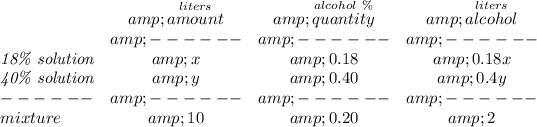
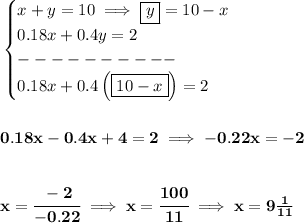
how much of the 40% solution? well y = 10 - x