Question

A cell phone store sells the basic model of a phone for $30 and the upgraded model for $100 when a customer signs a two-year agreement. On Tuesday, the store has $900 in sales. The store pays $5 for each basic model and $25 for each upgraded model. If the cost of the cell phones sold on Tuesday is $200, how many upgraded models were sold?

a 6 phones
b 10 phones
c 15 phones
d 42 phones

Answer 1

6 is correct if im not wrong

Answer 2

We will use a system of equations to solve this. Let x be the number of basic phones sold and y be the number of upgraded phones sold. The equation to represent the sales would be
30x + 100y = 900 (because each basic phone sells for $30 and each upgraded phone sells for $100, and the store did $900 in sales that day).
The equation to represent the cost to the store would be
5x + 25y = 200 (because each basic phone costs the store $5 and each upgraded phone costs the store $25, and the store had a cost of $200 that day).

`\left \{ {{30x+100y=900} \atop {5x+25y=200}} \right.`
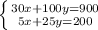
We will use elimination to solve this. Make the coefficients of x the same by multiplying the bottom equation by 6:

`\left \{ {{30x+100y=900} \atop {6(5x+25y=200}} \right. \\ \\ \left \{ {{30x+100y=900} \atop {30x+150y=1200}} \right.`
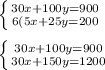
Now we can eliminate the x's by subtracting:

`\left \{ {{30x+100y=900} \atop {-(30x+150y=1200)}} \right. \\-------- \\-50y=-300`
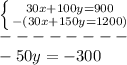
Divide both sides by 50:

`(50y)/(50)= (300)/(50) y=6`
There were 6 upgraded phones sold on Tuesday.