Question

I need help with this equation! Carbon-14 has a half-life of 5730 years. Derek has a sample of a fossil that has 33mg of its original 100 mg of carbon-14. Find the decay constant, k, and use it to answer the questions that follow.

First use the formula P(t)=Ae ^{kt} , to find the decay constant, k

Answer 1

First all, the decay formula is
`P(t)=Ae^(-kt)`
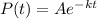
where:

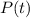
`P(t)` is the remaining quantity after
`t` years

`A` is the initial sample

`t` is the time in years

`k` is the decay constant

From the problem we know that
`A=33` and
`P=100`, but we don't have the time
`t`; to find it we will take advantage of the half-life of the Carbon-14. If you have a sample of 100 mg and Carbon-14 has a half-life of 5730, after 5730 years you will have half of your original sample i.e. 50 mg. We also know that after
`t` years we have a remaining sample of 33mg, so the amount of the sample that decayed is
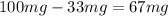
`100mg-33mg=67mg`. Knowing all of this we can set up a rule 3 and solve it to find
`t`:

`(100mg--\ \textgreater \ 5730years--\ \textgreater \ 50mg)/(100mg--\ \textgreater \ (t)years---\ \textgreater \ 67mg)`

`(5730years--\ \textgreater \ 50mg)/((t)years---\ \textgreater \ 67mg)`

`(5730)/(t) = (50)/(67)`

`t= ((5730)(67))/(50)`

`t=7678.2`

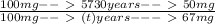
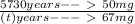
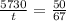
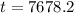
Now that we know our time
`t` lets replace all the values into our decay formula:

`33=100e^(-7678.2k)`
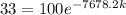
Notice that the constant
`k` we need to find is the exponent; we must use logarithms to bring it down, but first lets isolate the exponential expression:

`(33)/(100) = e^(-7678.2k)`

`e^(-7678.2k) = (33)/(100)`

`ln(e^(-7678.2k) )=ln( (33)/(100) )`

`-7678.2k=ln( (33)/(100) )`

`k= (ln( (33)/(100)) )/(-7678.2)`

`k=-0.000144`

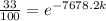
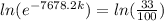
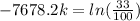
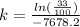
We can conclude that the decay constant
`k` is approximately -0.000144