This is an interesting problem involving astronomy, in fact, simple physics.
Let r=distance of sun to mars, in metres
Mars had an orbital period of 1.88 years.
=>
tangential velocity, v, of the planet, in m/s is
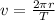
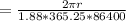 m/s, accounting for leap years
m/s, accounting for leap years
 m/s
m/s
The centripetal force, Fc, generated is

where m=mass of mars = 6.39*10^(24) kg
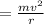
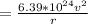
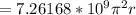
The gravitation pull from the sun, Fg, is given by
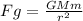
where G=grav. const., =6.67408*10^(-11) m^3 kg^(-1) s^(-2)
M=mass of sun=1.989*10^(30) kg
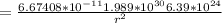
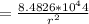
Since the radial distance is in equilibrium, the average distance, r can be found by equation Fc=Fg and solving for r:
Fc=Fg
=>
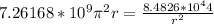
Solving for the real root:
![r^3=(8.48256*10^44)/(7.26168*10^9*%pi^2)]()
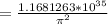
=2.279*10^11 m