Question

Consider the diagram and the paragraph proof below. Given: Right △ABC as shown where CD is an altitude of the triangle Prove: a2 + b2 = c2 Because △ABC and △CBD both have a right angle, and the same angle B is in both triangles, the triangles must be similar by AA. Likewise, △ABC and △ACD both have a right angle, and the same angle A is in both triangles, so they also must be similar by AA. The proportions and are true because they are ratios of corresponding parts of similar triangles. The two proportions can be rewritten as a2 = cf and b2 = ce. Adding b2 to both sides of first equation, a2 = cf, results in the equation a2 + b2 = cf + b2. Because b2 and ce are equal, ce can be substituted into the right side of the equation for b2, resulting in the equation a2 + b2 = cf + ce. Applying the converse of the distributive property results in the equation a2 + b2 = c(f + e).

Answer 1

The answer is B.

This is because since f + e = c,
then a² + b² = c(f + e)
a² + b² = c(c)
a² + b² = c²

This is the correct answer

Answer 2

Because f+e=c

Therefore ,
`a^2+b^2=c^2`

Explanation:

Given A right triangle ABC as shown in figure where CD is an altitude of the triangle.

To prove that
`a^2+b^2=c^2`

Proofe: Given
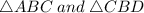`\triangle ABC\; and\; \triangle CBD` both are right triangle and both triangles have common angle B si same.

Therefore , two angles of two triangles are equal .

Hence,
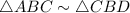`\triangle ABC \sim\triangle CBD` by using AA similarity.

Similarity property: when two triangles are similar then their corresponding angles are equal and their corresponding side are in equal proportion.

`(a)/(f) =(c)/(a)`

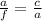
Similarly ,
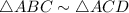`\triangle ABC \sim \triangle ACD` by AA similarity property . Because both triangles are right triangles therefore, one angle of both triangles is equal to 90 degree and both triangles have one common angle A is same .

`\therefore`
`(b)/(c) =(e)/(b)`

The corresponding parts of two similar triangles are in equal proportion therefore , two proportion can be rewrite as

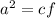`a^2=cf` (I equation)

and
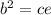`b^2=ce` (II equation)

Adding
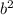`b^2` to both sides of firs equation

`a^2+b^2=cf+b^2`

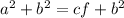
Because
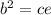`b^2=ce` and ce can be substituted into the right side of equation wevcan write as

`a^2+b^2=ce+cf`

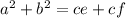
Applying the converse of distributive property we can write

`a^2+b^2=c(f+e)`

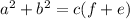
Distributive property: a.(b+c)= a.c+a.b

`a^2+b^2=c^2`

Because f+e=
`c^2`

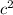
Hence proved.