Question

What is the 32nd term of the arithmetic sequence where a1 = −33 and a9 = −121? −396 −385 −374 −363

Answer 1

The formula to find the general term of an arithmetic sequence is,

`a_(n) =a_(1) +(n-1)d`

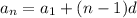
Where
`a_(n)`= nth term and

`a_(1)` = First term.

Given, a9 = −121. Therefore, we can set up an equation as following:

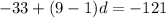`-33+(9-1)d = -121` Since, a1 = -33

- 33 + 8d = -121

-33 + 8d + 33 = -121 + 33 Add 33 to each sides of the equation.

8d = -88.

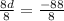`(8d)/(8) =(-88)/(8)` Divide each sides by 8.

So, d = - 11.

Now to find the 32nd terms, plug in n = 32, a1 = -33 and d = -11 in the above formula. So,

`a_(32) = -33 +(32 -1) (-11)`

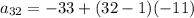
= -33 + 31 ( -11)

= - 33 - 341

= -374

So, 32nd term = - 374.

Hope this helps you!