Question

Solve the following system of equations

5x-2y=4
8x+5y=-10

Answer 1

`5x - 2y = 4 \\ 5x = 4 + 2y \\ (5x)/(5) = (4 + 2y)/(5) \\ x = (4 + 2y)/(5) ......(3)equation`

NOTE I AM SOLVING BY SUBSTITUTION

`8( (4 + 2y)/(5) ) + 5y = - 10 \\ (32 + 16y)/(5 ) + 5 y = - 10 \\ (32 + 16y)/(5) (5) + 5y(5) = - 10(5) \\ 32 + 16y + 25y = - 50 \\ 41y = - 50 - 32 \\ \\ \\ \\ 41y = - 82 \\ ( - 41y)/(41) = ( - 82)/(41) \\ y = - 2`

`x = (4 + 2( - 2))/(5) \\ x = (4 - 4)/(5) \\ x = (0)/(5) \\ x = 0`

ATTACHED IS THE SOLUTION

Answer 2

Answer: (0,-2)

Explanation:

`\displaystyle\\\left \{ {{5x-2y=4\ \ \ \ \ (1)} \atop {8x+5y=-10\ \ (2)}} \right.`

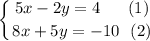
Multiply equation (1) by 5, and equation (2) by 2:

`\displaystyle\\\left \{ {{25x-10y=20\ \ \ \ (3)} \atop {16x+10y=-20\ \ (4)}} \right.`

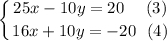
Add equations (3) and (4):

`41x=0`

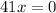
Divide both parts of the equation by 41:

`x=0`

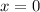
Let's substitute the value of x into equation (2):

`8(0)+5y=-10\\0+5y=-10\\5y=-10`

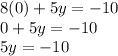
Divide both parts of the equation by 5:

`y=-2`

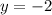
Thus, (0,-2)