Answer:
Last term is 1,527,890.
Explanation:
In this question a geometric series has been given with
first term A = 23
6th term = 1,358,127
Number of terms n = 6
we have to calculate the sum of this geometric series
we know
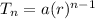

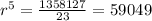
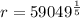
r = 9
Now we know the formula to sum a geometric series is
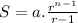
S = 23 ×

S = 23 ×
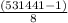
S =
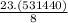 = 23 × 66430
= 23 × 66430
S = 1,527,890