Question

when an aircraft takes off, it accelerates until it reaches its takeoff speed V. in doing so it uses up a distance R of the runway, where R is proportional to the square of the of the takeoff speed. if V is measured in miles per hour and R is measured in feet, then 0.1639 is the constant of proportionality. if an aircraft has a takeoff speed of about 215 miles per hour, how much runway does it need?

Answer 1

Answer: 36.22 feet

Step-by-step explanation:

Two quantities are proportional if and only if their ratio is constant. Since V and the square of R are proportional, then the ratio of V to the square of R is constant. In terms of equation:


`(V)/(R^2) = k`

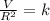
For some constant k.

Since the constant of proportionality is equal to 0.1639, k = 0.1639. Moreover, since the takeoff speed of the aircraft needs to be 215 miles per hour, the runway needed is will be obtained by solving for R in the following equation:


`(V)/(R^2) = k \\ \\ V = kR^2 \\ \\ R^2 = (V)/(k) \\ \\ R = \sqrt{(V)/(k)} \\ \\ R = \sqrt{(215)/(0.1639)} \\ \\ \boxed{R = 36.22 \text{ feet}}`

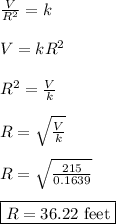
Hence, a runway of 36.22 feet is needed for the aircraft to have a takeoff speed of 215 miles per hour.