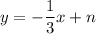Question

Convert the parametic equation x(L)=2-3t and y(t)=4+L into slope intercept form

Answer 1

I guess those 'L' are 't'.

Solve for t in both parametric equations:


`x(t) = 2 - 3t \iff t = (x-2)/(-3)`


`y(t)=4+t \iff t = y-4`

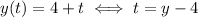
Now, you have two expressions for t. The must be equal to each other:


`(x-2)/(-3) = y - 4`

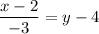
Solve for y in this last equation:


`y = (x-2)/(-3) + 4 = -(1)/(3)x+(14)/(3)`

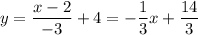
And you've got the slope-intercept form.

Yo could also find from the beginning the slope: it's the quotient of the coefficients of the parameter:


`m = (1)/(-3)`

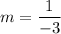
And, then find the intercept by plugging the point (2,4) into the equation:


`y=-(1)/(3)x+n`