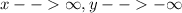Question

Describe the end behavior of the function f(x) = 3 − 4x + 6x2 − 5x3.

Answer 1

Ends up in Quadrants II and IV

Explanation:

Since the leading coefficient is −5 and the degree is 3, the function has the behavior described.

Answer 2

we are given

`f(x)=3-4x+6x^2-5x^3`

we can see that this is polynomial

so, firstly we will find degree and leading coefficients

Degree:

It is the highest exponent of the polynomial

highest exponent is 3

so, degree=3

which is odd

Leading coefficient:

It is the constant term multiplied to highest exponent term

we can see that

constant term is -5

so, leading coefficient is -5

which is negative

End behavior:

degree is odd and leading coefficient is negative

so, it rises to left and falls to right

or we can also write as

`x-->-\infty, y-->\infty`

`x-->\infty, y-->-\infty`