We are given 158 books to place them on three different shelves like A, B, and C.
It says that shelf A has eight fewer books than shelf B and five more books than shelf C.
Mathematically, it can be written as (A = B - 8) and (A = C + 5).
Or we can write it as (B = A + 8) and (C = A - 5).
If we consider there are 'x' books in shelf A, then shelf B would have 'x+8' books and shelf C would have 'x-5' books.
We know that Total books are 158, so its sum must be equal to total books.
A + B + C = 158
x + (x+8) + (x-5) = 158
3x + 3 = 158
3x + 3 - 3 = 158 - 3
3x = 155
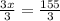
x = 51.667 books
But 'x' must be an integer value because number of books can not be a decimal form.
Hence, this arrangement is "NOT possible" for this question.