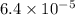Answer : The value of
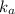 for benzoic acid is,
for benzoic acid is,
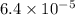
Solution :
The balanced equilibrium reaction will be,
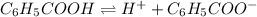
initial conc. 0.2 M 0 0
at eqm.
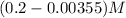
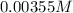
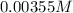
The expression for dissociation constant for a benzoic acid will be,
![k_a=([H^+]* [C_6H_5COO^-])/([C_6H_5COOH])](https://img.qammunity.org/2019/formulas/chemistry/college/cee1arpucd0w8xhadewzlnew0xt3z3sm7s.png)
Now put all the given values in this formula, we get the value of
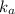
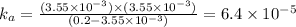
Therefore, the value of
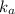 for benzoic acid is,
for benzoic acid is,