Hi! This problem follows the binomial distribution where there are only two outcomes - either Sandra gets a ride to work or not. A binomial distribution is modeled by the following equation:
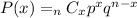
where p is the probability of success for x trials and q is the probability of failure (n is the total number of trials). In the case of the problem p would be the probability of getting a ride which is equal to 0.7 while q would be 0.3.
To find the probability that she successfully gets a ride 3 out of 5 times, we just substitute 3 as the value of x:
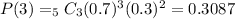
Meanwhile, to find the probability that she gets AT LEAST 2 out of 5 rides, we just get the probability that she gets 1 ride or no ride at all then subtract the sum of these two probabilities from 1.
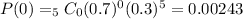
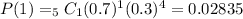
![P(x \geq 2)=1-[P(0)+P(1)]=1-(0.00243+0.02835)=1-0.03078](https://img.qammunity.org/2019/formulas/advanced-placement-ap/middle-school/eq67nk5rfmt6xye2ssovn84v5bkcpa9sr8.png)
 ANSWER:
ANSWER: The probability that Sandra gets a ride 3 times in a 5-day work is 0.309, and the probability that she gets a ride at least 2 times in a 5-day work is 0.969.