Question

Help please! 10 points!

10: Gavin builds furniture for a living. he Sells chairs for $45 and tables for $70 each. It takes Gavin 4 hours and $10 worth of supplies to build each chair. A table requires 10 hours and $15 worth of supplies to make. Gavin wants to work for no more than 40 hours per week and spend no more than $80 on materials. Write a system of inequalities and state 3 possible combos.

Answer 1

Let the number of chairs Gavin build per week is x and number of tables he builds per week is y.

It takes 4 hours to work on a chair and 10 hours to work on a table. So time taken to work on x chairs and y tables will be:


`Time=4x+10y`

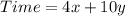
Gavin wants to work for no more than 40 hours. So we can write the inequality as:


`4x+10y \leq 40`

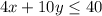
It takes $10 worth of supplies to build a chair and $15 worth of supplies to build a table. So cost or worth of supplies for x chairs and y tables will be:


`Cost=10x+15y`

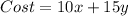
Gavin wants to spend no more than $80 on material. So we can write the inequality as:


`10x+15y \leq 80`

Thus the system of inequalities is:


`4x+10y \leq 40`

`10x+15y \leq 80`

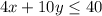
We can observe the possible combinations from the graph of these inequalities, which is shown below:
a) 0 chair and 3 tables
b) 5 chairs and 2 tables
c) 8 chairs and 2 tables