Answer:
Option: A is the correct answer.
A. The graph of f(x) is shifted four units down from the graph of g(x).
Explanation:
We know that for any parent function g(x) the transformed function g(x)+k is a shift of the function g(x) k units up or down depending on the value of k
i.e. if k>0 then the shift is k units up
and if k<0 then the shift is k units down.
Hence, here we have parent function g(x) as:
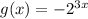
and we are given transformed function f(x) as:

This means we have k=-4<0
This means that the function f(x) is the shift of the parent function g(x) 4 units down.