Question

Which of the following is an odd function?

g(x) = x2
g(x) = 5x – 1
g(x) = 3
g(x) = 4x

Answer 1

An odd function is symmetrical about the origin: g(-x) = -g(x).

The 4th selection is appropriate.

Answer 2

g(x) = 4x is an odd function.

Explanation:

A function g(x) is odd if it satisfies that, for all x we have g(-x) = -g(x). Then,

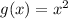`g(x) =x^2` is not an odd function beacuse only give positive values, then for example if x= 2

`g(-2) =(-2)^2 = 4 \\eq -4 = -g(2)`.

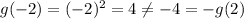g(x) = 5x-1 is not an odd function. I'll also give you a counterexample: for x=1 we have

g(-1) = 5(-1)-1 = -6 ≠ -4 = -(5-1) = -g(1).

g(x) = 3 is not an odd function. I'll also give you a counterexample: for x=1 we have

g(-1) = 3 ≠ -3 = -g(1).

Finally, g(x) = 4x is an odd function because for all x we have g(-x) = -g(x):

g(-x) = 4(-x) = -4x = -g(x).