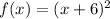Question

Heather is writing a quadratic function that represents a parabola that touches but does not cross the x-axis at x = –6. Which function could Heather be writing?

Answer 1

The equation is
`y= (x-6) ^(2)`. I hope this helps.

Answer 2

`f(x)=(x+6)^2`

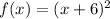
Explanation:

We have been given that the parabola touches the x-axis at the zero x = -6.

Whenever, the graph touches the x axis at any zero and returns back then the multiplicity of that zero is even.

On the other hand if the graph crosses the x axis at any zero then the multiplicity of the zero will be odd.

Now, parabola touches the x-axis at the zero x = -6 hence, the multiplicity of the zero is even. Since, it is a quadratic function hence, the multiplicity will be 2.

The zero is x = -6 hence, the factor would be (x+6).

Therefore, the function is
`f(x)=(x+6)^2`