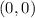Answer:
The center of circle is
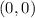
Explanation:
We need to find the center of the circle of the equation
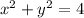
Since, the general equation of circle is
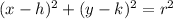
Where (h,k) is center of circle and r is radius.
Re-write the circle equation is
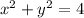 as,
as,
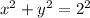
Compare
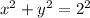 with
with
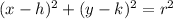
so,
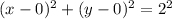
Hence, the center of circle is