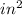Question

Help I'm taking a k12 quiz 2.04: composite figures but, I can't figure these out can anyone help me?

Question. 1 What is the area of this polygon? (Picture 1)
Question. 2 What is the area of this polygon? 42.5 Units? 41.5 Units? 35.5 Units? 29.5 Units? (Picture 2)
Question. 3 This figure is made up of a rectangle and parallelogram.

What is the area of this figure? (Picture 3)
Question. 4 What is the area of this composite shape? (Picture 4)

Thank you angels who help me with these

Answer 1

All of these can be solved by separating complex figur into simpler one.
Needed formulas are:
Area of rectangle A=a*b
Area of triangle A=a*h/2
Area of paralelogram A= a*h

QUESTION 1.
When we connect points F and S we get a rectangle and a triangle.
Dimensions of sides of a rectangle are a=9 and b=2.
A=9*2=18
`units^(2)`
For a triangle we need to take one side and it's height. Let's take side FS because it's easiest to find the height.
a=9
h=6
A=9*6/2=27
`units^(2)`

Tot+al area of a figure:
A=18+27=45
`units^(2)`

QUESTION 2.
We connect point (1,1) with (1,-2) and (-6,1). This way we get a rectangle and three triangles.
Rectangle:
a=3
b=4
A=3*4=12
`units^(2)`

Top right triangle:
a=4
h=3
A=4*3/2=6
`units^(2)`

Top left triangle:
a=7
h=2
A=7*2/2=7
`units^(2)`

Bottom left triangle:
a=7
h=3
A=7*3/2=10.5
`units^(2)`

Total area of a figure:
A=12+6+7+10.5=35.5
`units^(2)`

QUESTION 3.
We connect points (-4,2) and (-1,3). This way we get a paralelogram and a rectangle.

Paralelogram:
a=6
h=1
A=6*1=6
`units^(2)`

Rectangle:
a=distance between (-4,2) and (-1,3) =
`\sqrt{ (-1-(-4))^(2) + (3-2)^(2) } = √(10)`
b = distance between (-4,2) and (-2,-4) =
`\sqrt{ (-2-(-4))^(2) + (-2-2)^(2) } = √(20)`
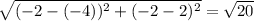
A=a*b=
`√(10) * √(20) = √(200) =10 √(2)`
`units^(2)`

Paralelogram:
a=6
h=1
A=6*1=6
`units^(2)`

Total area of a figure:
A=
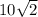
`10 √(2)` + 6
`units^(2)`

QUESTION 4.
We coonect missing side of a triangle. That side has a length of: 6in-3in=3in. Vertical side of triangle is: 13in-7in=6in
Area:
a=3
h=6
A=3*6/2=9
`in^(2)`

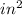
Rectangle:
a=7in
b=6in
A=7*6=42
`in^(2)`

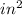
Total area of a figure:
A=9+42=51
`in^(2)`