The electric field generated by an uniformly charged wire at a distance r from the wire is given by
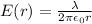
where
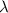
is the linear density of charge and
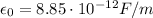
is the electric permittivity.
In our problem, the charge density is
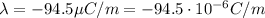
. We want to calculate the electric field at
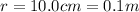
, which is
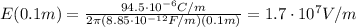
and since the charge on the wire is negative, the field points toward the wire.