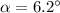Question

What are the magnitude and direction of the force the pitcher exerts on the ball? (enter your magnitude to at least one decimal place.)?

Answer 1

The answer should be 6.2

Answer 2

Details are missing in the question. Complete text of the problem:

"The gravitational force exerted on a baseball is 2.28 N down. A pitcher throws the ball horizontally with velocity 16.5 m/s by uniformly accelerating it along a straight horizontal line for a time interval of 181 ms. The ball starts from rest.

(a) Through what distance does it move before its release? (m)
(b) What are the magnitude and direction of the force the pitcher exerts on the ball? (Enter your magnitude to at least one decimal place.)"

Solution

(a) The pitcher accelerates the baseball from rest to a final velocity of
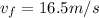`v_f = 16.5 m/s`, so
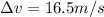`\Delta v=16.5 m/s`, in a time interval of
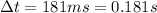`\Delta t = 181 ms=0.181 s`. The acceleration of the ball in the horizontal direction (x-axis) is therefore

`a_x = (\Delta v)/(\Delta t)= (16.5 m/s)/(0.181 s)=91.2 m/s^2`

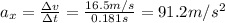
And the distance covered by the ball during this time interval, before it is released, is:

`S= (1)/(2) a_x (\Delta t)^2 = (1)/(2) (91.2 m/s^2)(0.181 s)^2=1.49 m`

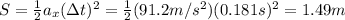
(b) For this part we need to consider also the weight of the ball, which is
`W=mg=2.28 N`

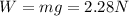
From this, we find its mass:
`m= (W)/(g)= (2.28 N)/(9.81 m/s^2)=0.23 Kg`

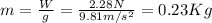
Now we can calculate the magnitude of the force the pitcher exerts on the ball. On the x-axis, we have

`F_x = m a_x = (0.23 kg)(91.2 m/s^2)=20.98 N`

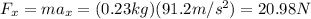
We also know that the ball is moving straight horizontally. This means that the vertical component of the force exerted by the pitcher must counterbalance the weight of the ball (acting downward), in order to have a net force of zero along the y-axis, and so:

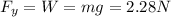`F_y=W=mg=2.28 N` (upward)

So, the magnitude of the force is

`F= √(F_x^2+F_y^2)= √((20.98N)^2+(2.28N)^2)=21.2 N`

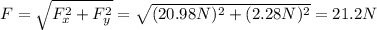
To find the direction, we should find the angle of F with respect to the horizontal. This is given by

`\tan \alpha = (F_y)/(F_x)= (2.28 N)/(20.98 N)=0.11`

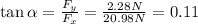
From which we find
`\alpha=6.2^(\circ)`