First, we need to define the function of (fog)(x)(fog)(x) = f(g(x))
it means we need to substitute the x in the function f(x) with g(x)
f(x) = x + 7
change x with g(x)
fog(x) = g(x) + 7
fog(x) =
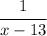
+ 7
equalize the denominators
fog(x) =
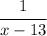
+ 7
fog(x) =
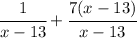
simplify
fog(x) =
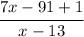
fog(x) =
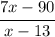 Second, determine the domain of the function
Second, determine the domain of the functionIf the function is in fraction form, the denominator of the fraction can't be equal to zero.
x - 13 ≠ 0
x ≠ 13
The domain is x
The answer is last option