Question

(fog)(x) and (gof)(x)
f(x)= 8/1-5x
g(x)= 1/x

Then find the domain for each

Answer 1

To find FoG ( or F of G) you put the equation of G in for the X of F

FoG =
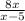
`(8x)/(x-5)` The domain is All Except 5 since it makes the bottom 0

GoF =
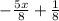
`- (5x)/(8) + (1)/(8)` The domain is -Infinity to Infinity


FoG --- The picture --- You want the denominator the same for both of the numbers. By turning 1 into 1x/x it still stays 1 because the x's cancel out, but it can group with the 5.

Next you can multiply both sides (top and bottom) by x and get the final product.

GoF --- Multiply both sides by 5x+1 and get the final product