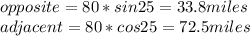Question

From a top-down 2D perspective, a car moves in a diagonal line and travels a distance equivalent to 80 miles. If the angle between the diagonal line and a horizontal reference line is 25 degrees, how far did the car travel horizontally and vertically? If necessary, round your answers to the nearest tenth of a mile. Horizontal distance? Vertical distance?

Answer 1

We can use Pythagorean theorem for right angle triangle to solve this problem.

The diagonal line would be hypothenuze. Horizontal and vertical distance would be other two sides of a triangle.

We will use the following formulas:

`sin \alpha = (opposite)/(hypothenuze) \\ cos \alpha = (adjacent)/(hypothenuze)`
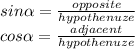
Where opposite side is vertical distance and adjacent side is horizontal distance.

Solving for these two sides we have:

`opposite = hypothenuze * sin \alpha \\ adjacent = hypothenuze * cos \alpha`

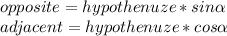
We insert numbers and we get solution:

`opposite = 80 * sin 25 = 33.8miles \\ adjacent = 80 * cos 25 = 72.5miles`