Question

Hey, I need some serious help with this math question!

Joe can more 6 acres in 5 hours. Sara can do the same job in 4 hours because she has a wide lawnmower. If they work together at their normal rate of work, how long will it the them too finis? I need help setting up the problem and then solving it... Please help!

Answer 1

It would take them about 2 hours to do it

Answer 2

so Joe can mow the 6 acres in 5 hours, whilst Sara can do it in only 4 hours. So in after 1 hour of working, Joe has only done 1/5 of the whole thing, and after working for 1 hour as well, Sara has however done 1/4 of the whole job.

let's say they both work together and do it in "t" hours.

now, after one hour has passed, Joe has done 1/5 of the whole thing, and Sara has done 1/4 of it, and since the job took "t" hours, after 1 hour it has only being done 1/t thus far, thus


`\bf \stackrel{Joe}{\cfrac{1}{5}}~~+~~\stackrel{Sara}{\cfrac{1}{4}}~~=~~\stackrel{total~thus~far}{\cfrac{1}{t}} \\\\\\ \cfrac{4+5}{20}=\cfrac{1}{t}\implies 9t=20\implies t=\cfrac{20}{9}\implies t=2(2)/(9)`

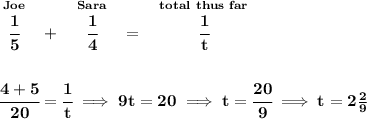
which is 2 hours 13 minutes and about 20 seconds.