Question

The half-life of a radioactive substance is the average amount of time it takes for half of its atoms to disintegrate. Suppose you started with 200 grams of a substance with a half-life of 3 minutes. How many minutes have passed if 25 grams now remain? Explain your reasoning.

Answer 1

3 half-lives because 200/2=100 100/2=50 and 50/2=25 

Answer 2

It would take 9 minutes for 25 grams of the substance to remain.

Explanation:

Radioactive substance degenerate to release particles and lot of energy. The time required for a radioactive substance to degenerate into half of its original size is termed half life. The substance continues the stages of degeneration with respect to the half life.

The given substance would have 3 stages of degeneration to achieve a mass of 25 grams with respect to the half life.

1st stage, it would degenerate to half of its original size;

=
`(200)/(2)`

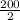
= 100 grams

This occurs in 3 minutes.

2nd stage, it would degenerate to half of its previous size;

=
`(100)/(2)`

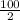
= 50 grams

This also occurs in 3 minutes.

3rd stage, it would degenerate to half of it previous size;

=
`(50)/(2)`

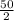
= 25 grams

This also occurs in 3 minutes.

We stop here due to the restriction in the question for 25 grams.

So, the total time taken for the substance to reach a mass of 25 grams

= 3 + 3 + 3

= 9 minutes

It would take 9 minutes for 25 grams of the substance to remain.