Question

Which is one of the transformations applied to the graph of f(x) = x2 to change it into the graph of g(x) = 4x2 + 24x + 30?

The graph of f(x) = x2 is widened.
The graph of f(x) = x2 is shifted left 3 units.
The graph of f(x) = x2 is shifted up 30 units.
The graph of f(x) = x2 is reflected over the x-axis.

Answer 1

The graph of f(x) = x2 is shifted left 3 units.

Answer 2

The graph is shifted left 3 units.

We know that the graph of f(x) is NOT widened, because for a number c greater than 1, cf(x) stretches the graph vertically, not horizontally.

We know that the graph of f(x) is NOT shifted up 30 units. It is tempting to say this because we do see +30 as the last term. But, we have to calculate the vertex of g(x). If we find the point
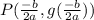
`P( (-b)/(2a), g((-b)/(2a)))`, that is, by taking doing
`(-24)/(2*4) = -3`,
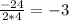
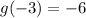
`g(-3)=-6`, we see that the vertex is six units down from f(x), not 30 units up!

We know that the graph of f(x) is NOT reflected over the x-axis, because there would need to a negative coefficient on the
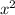
`x^2`-term, and there isn't.

We know that the graph of f(x) IS shifted 3 units to the left. When we calculated the vertex earlier, we saw that it is
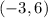
`(-3,6)`, which indeed corresponds to a shift 3 units to the left from the origin.